
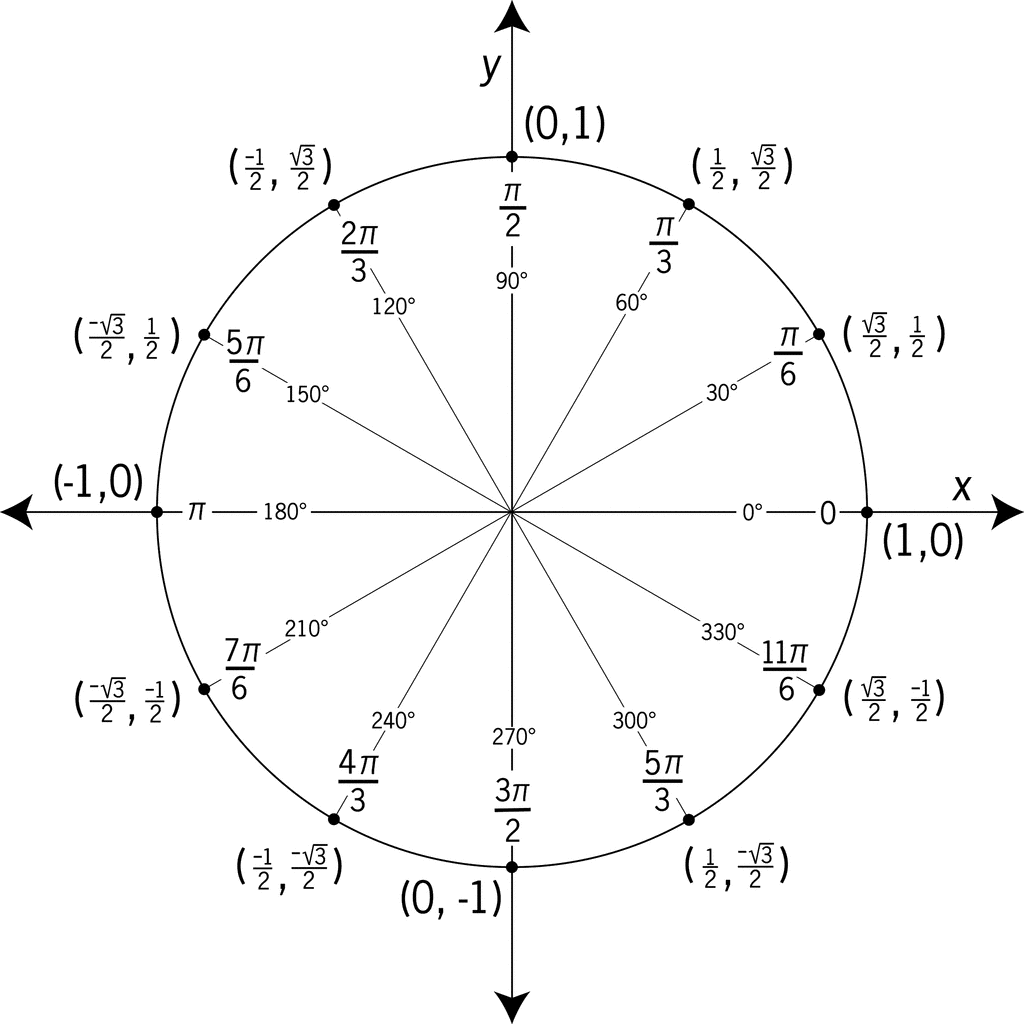
Likewise, there will be an angle in the fourth quadrant with the same cosine as the original angle. Therefore, its cosine value will be the opposite of the first angle’s cosine value. Because the sine value is the y-coordinate on the unit circle, the other angle with the same sine will share the same y-value, but have the opposite x-value. We have discussed finding the sine and cosine for angles in the first quadrant, but what if our angle is in another quadrant? For any given angle in the first quadrant, there is an angle in the second quadrant with the same sine value. The bounds of the x-coordinate are\,\left.\,The bounds of the y-coordinate are also\,\left.\,Therefore, the range of both the sine and cosine functions is\,\left. What are the ranges of the sine and cosine functions? What are the least and greatest possible values for their output? We can see the answers by examining the unit circle, as shown in (Figure). The input to the sine and cosine functions is the rotation from the positive x-axis, and that may be any real number. The four quadrants are labeled I, II, III, and IV.įor any angle\,t,we can label the intersection of the terminal side and the unit circle as by its coordinates,\,\left(x,y\right).\,The coordinates\,x\,and\,y\,will be the outputs of the trigonometric functions\,f\left(t\right)=\mathrm\,r,there is no lower or upper limit to the angles that can be inputs to the sine and cosine functions. We label these quadrants to mimic the direction a positive angle would sweep. The x- and y-axes divide the coordinate plane into four quarters called quadrants. The angle (in radians) that\,t\,intercepts forms an arc of length\,s.\,Using the formula\,s=rt,and knowing that\,r=1,we see that for a unit circle,\,s=t. Recall that a unit circle is a circle centered at the origin with radius 1, as shown in (Figure). In this section, we will redefine them in terms of the unit circle. We have already defined the trigonometric functions in terms of right triangles. Finding Trigonometric Functions Using the Unit Circle


 0 kommentar(er)
0 kommentar(er)
